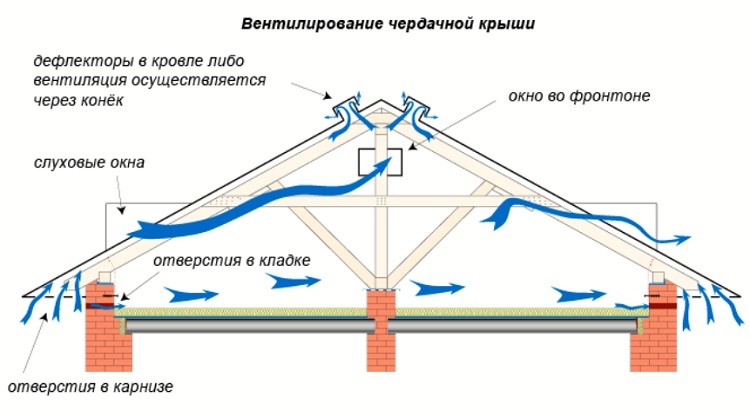
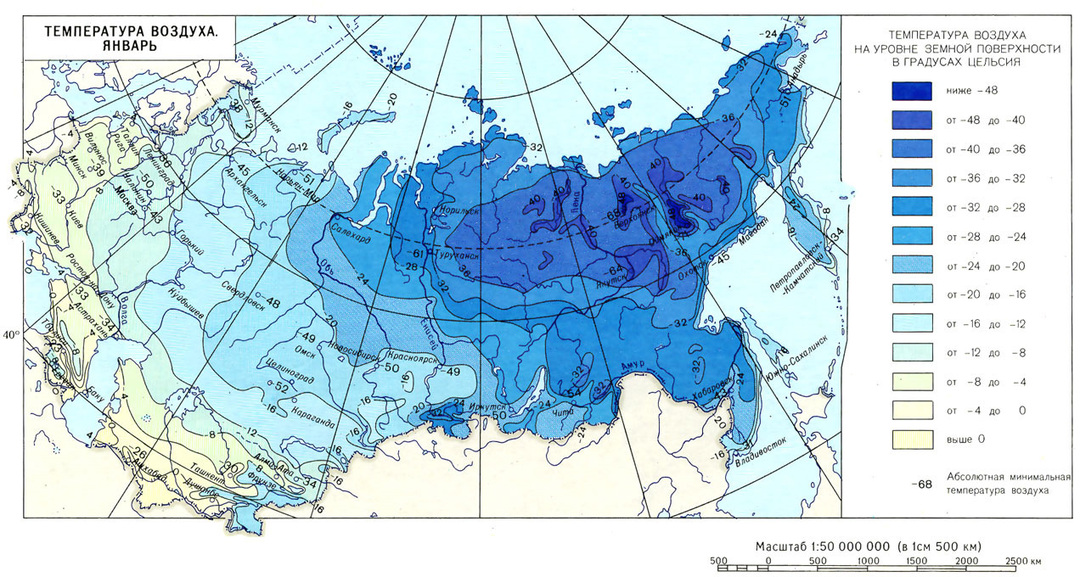
Eiere av mellomstore og store hytter bør planlegge vedlikeholdskostnadene. Derfor oppstår ofte oppgaven med å beregne gassforbruket for oppvarming av et hus 200 m2 eller større område. Den originale arkitekturen tillater vanligvis ikke å bruke analogimetoden og finne ferdige beregninger.
Det er imidlertid ikke nødvendig å betale penger for denne oppgaven. Alle beregninger kan gjøres selv. Dette vil kreve kunnskap om noen forskrifter, samt forståelse for fysikk og geometri på skolenivå.
Vi vil hjelpe deg å forstå dette viktige spørsmålet for husøkonomen. Vi viser deg hvilke formler som brukes til å beregne, hvilke egenskaper du trenger å vite for å få resultatet. Artikkelen som presenteres av oss gir eksempler på grunnlag av hvilke det blir lettere å lage din egen beregning.
Innholdet i artikkelen:
-
Finne mengden energitap
- Termisk ledningsevne og termisk motstand mot materialet
- Beregning av varmetap gjennom innelukkende konstruksjoner
- Typisk vegg- og takgeometri
- Varmetap gjennom gulv og fundament
- Regnskap for uoppvarmede lokaler
- Kjøling gjennom ventilasjon
- Beregning av gassforbruk
- Eksempel på en hytte på 200 m2
- Konklusjoner og nyttig video om temaet
Finne mengden energitap
For å bestemme mengden energi som et hus mister, er det nødvendig å kjenne de klimatiske egenskapene til området, termisk ledningsevne til materialer og ventilasjonshastigheter. Og for å beregne det nødvendige gassvolumet, er det nok å vite dens brennverdi. Det viktigste i dette arbeidet er oppmerksomhet på detaljer.
Oppvarming av bygningen må kompensere for varmetap som oppstår av to hovedårsaker: varmelekkasje rundt omkretsen av huset og tilstrømning av kald luft gjennom ventilasjonssystemet. Begge disse prosessene er beskrevet med matematiske formler, ifølge hvilke du uavhengig kan utføre beregninger.
Termisk ledningsevne og termisk motstand mot materialet
Ethvert materiale kan lede varme. Intensiteten til overføringen uttrykkes gjennom koeffisienten for varmeledningsevne λ (W / (m × ° C)). Jo lavere den er, desto bedre er strukturen beskyttet mot frysing om vinteren.
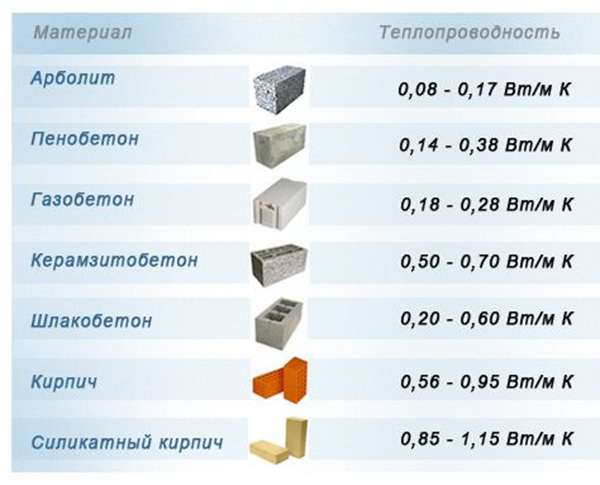
Varmeutgifter avhenger av varmeledningsevnen til materialet huset skal bygges av. Dette er spesielt viktig for de "kalde" områdene i landet.
Bygninger kan imidlertid brettes eller isoleres med materialer av varierende tykkelse. Derfor brukes i praktiske beregninger koeffisienten for motstand mot varmeoverføring:
R (m2 × ° C / W)
Det er relatert til varmeledningsevne med følgende formel:
R = h / λ,
hvor h - materialtykkelse (m).
Eksempel. La oss bestemme motstandskoeffisienten mot varmeoverføring av D700 luftbetongblokker med forskjellige bredder ved λ = 0.16:
- bredde 300 mm: R = 0.3 / 0.16 = 1.88;
- bredde 400 mm: R = 0.4 / 0.16 = 2.50.
Til isolasjonsmaterialer og vindusblokker kan gis både koeffisienten for varmeledningsevne og koeffisienten for motstand mot varmeoverføring.
Hvis den omsluttende strukturen består av flere materialer, blir koeffisientene til de individuelle lagene oppsummert når du bestemmer motstandskoeffisienten mot varmeoverføring av hele "paien".
Eksempel. Veggen er bygget av luftbetongblokker (λb = 0,16), 300 mm tykk. Utenfor er den isolert ekstrudert polystyrenskum (λs = 0,03) 50 mm tykk, og innsiden kledd med brett (λv = 0,18), 20 mm tykk.
Det er tabeller for forskjellige regioner, der minimumsverdiene for den totale varmeoverføringskoeffisienten for omkretsen av huset er foreskrevet. De er rådgivende i naturen.
Nå kan du beregne den totale motstandskoeffisienten mot varmeoverføring:
R = 0.3 / 0.16 + 0.05 / 0.03 + 0.02 / 0.18 = 1.88 + 1.66 + 0.11 = 3.65.
Bidraget til lag som er ubetydelig når det gjelder parameteren "varmebesparelse" kan neglisjeres.
Beregning av varmetap gjennom innelukkende konstruksjoner
Varmetap Sp (W) over en jevn overflate kan beregnes som følger:
Q = S × dT / R,
hvor:
- S - arealet av den vurderte overflaten (m2);
- dT - temperaturforskjell mellom innendørs og utendørs luft (° С);
- R - motstandskoeffisient mot varmeoverføring av overflaten (m2 * ° С / W).
For å bestemme totalindikatoren for alt varmetap, utfør følgende handlinger:
- tildele områder som er homogene når det gjelder motstandskoeffisienten mot varmeoverføring;
- beregne sine områder;
- bestem indikatorene for termisk motstand;
- utføre beregningen av varmetap for hver av seksjonene;
- oppsummer de oppnådde verdiene.
Eksempel. Hjørnerom 3x4 meter i toppetasjen med kaldt loftsrom. Den siste takhøyden er 2,7 meter. Det er 2 vinduer som måler 1 × 1,5 m.
La oss finne varmetapet gjennom omkretsen ved en lufttemperatur inne i "+25 ° С", og utenfor - "–15 ° С":
- La oss velge områder som er homogene når det gjelder motstandskoeffisient: tak, vegg, vinduer.
- Takområde SNS = 3 × 4 = 12 m2. Vindusområde SO = 2 × (1 × 1,5) = 3 m2. Veggområde Smed = (3 + 4) × 2.7 – SO = 29,4 m2.
- Takets termiske motstandskoeffisient består av overlappingsindeksen (brett med en tykkelse på 0,025 m), isolasjon (mineralullplater med en tykkelse på 0,10 m) og et tregulv på loftet (tre og kryssfiner med en total tykkelse på 0,05 m): RNS = 0.025 / 0.18 + 0.1 / 0.037 + 0.05 / 0.18 = 3.12. For vinduer er verdien hentet fra passet til et dobbeltvindu: RO = 0.50. For en vegg brettet som i forrige eksempel: Rmed = 3.65.
- SpNS = 12 × 40 / 3,12 = 154 W. SpO = 3 × 40 / 0,50 = 240 W. Spmed = 29,4 × 40 / 3,65 = 322 W.
- Generelt varmetap i modellrommet gjennom de omsluttende konstruksjonene Sp = SpNS + SpO + Spmed = 716 W.
Beregning i henhold til oppgitte formler gir en god tilnærming, forutsatt at materialet oppfyller de deklarerte varmeledende kvalitetene og det ikke er noen feil som kan gjøres under konstruksjonen. Eldring av materialer og konstruksjon av huset generelt kan også være et problem.
Typisk vegg- og takgeometri
De lineære parametrene (lengde og høyde) til strukturen når du bestemmer varmetap, er vanligvis å være interne, ikke eksterne. Det vil si at ved beregning av varmeoverføring gjennom materialet, blir kontaktområdet for varm, ikke kald luft tatt i betraktning.
Ved beregning av den indre omkretsen er det nødvendig å ta hensyn til tykkelsen på de indre partisjonene. Den enkleste måten å gjøre dette på er i henhold til husets plan, som vanligvis skrives ut på papir med et rutenett.
Således for eksempel med en husstørrelse på 8 × 10 meter og en veggtykkelse på 0,3 meter, den indre omkretsen Pint = (9,4 + 7,4) × 2 = 33,6 m, og den ytre Pute = (8 + 10) × 2 = 36 m.
Mellomgulv har vanligvis en tykkelse på 0,20 til 0,30 m. Derfor vil høyden på to etasjer fra gulvet til det første til taket til det andre fra utsiden være lik Hute = 2,7 + 0,2 + 2,7 = 5,6 m. Hvis du bare legger til etterbehandlingshøyden, får du en mindre verdi: Hint = 2,7 + 2,7 = 5,4 m. Mellomgulvet overlapper, i motsetning til veggene, har ikke funksjonen som isolasjon, derfor må du ta for beregninger Hute.
For hus i to etasjer med dimensjoner på ca 200 m2 forskjellen mellom veggene på innsiden og utsiden er fra 6 til 9%. På samme måte tar de indre dimensjonene hensyn til de geometriske parametrene til taket og gulvene.
Beregning av veggenes areal for enkle geometrihytter er elementær, siden fragmentene består av rektangulære seksjoner og pedimenter av lofts- og loftsrom.
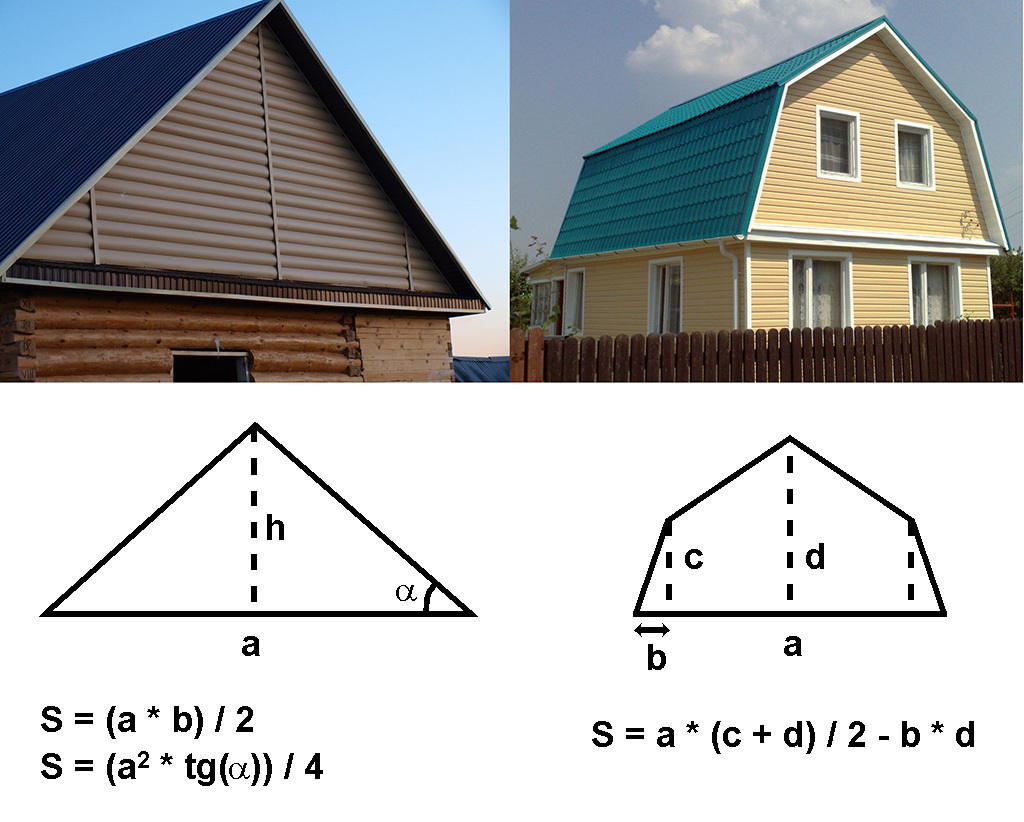
Gavlene på loft og loft har i de fleste tilfeller form av en trekant eller en femkant symmetrisk langs vertikalen. Å beregne området er ganske enkelt.
Ved beregning av varmetap gjennom taket er det i de fleste tilfeller tilstrekkelig å bruke formler for å finne områdene i en trekant, rektangel og trapes.
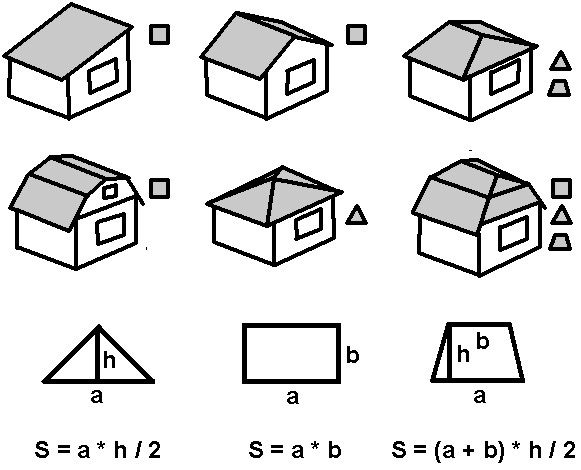
De mest populære takformene for private hus. Når du måler parametrene, må du huske at de interne dimensjonene er erstattet i beregningene (uten takfot)
Arealet av det lagt taket kan ikke tas når du bestemmer varmetapet, siden det også går til overhengene, som ikke tas i betraktning i formelen. I tillegg plasseres ofte materialet (for eksempel takpapir eller profilert galvanisert ark) med en liten overlapping.

Noen ganger ser det ut til at det er ganske vanskelig å beregne takarealet. Men inne i huset kan geometrien til det isolerte gjerdet i øverste etasje være mye enklere.
Den rektangulære geometrien til vinduene gir heller ikke problemer med beregninger. Hvis de doble vinduene har en kompleks form, kan området ikke beregnes, men læres av produktpasset.
Varmetap gjennom gulv og fundament
Beregning av varmetap i bakken gjennom gulvet i underetasjen, samt gjennom veggene og kjellergulvet, vurderes i henhold til reglene som er foreskrevet i vedlegg E i SP 50.13330.2012. Faktum er at varmeforplantningshastigheten i jorden er mye lavere enn i atmosfæren, så jord kan også betinget tilskrives et isolasjonsmateriale.
Men siden de er preget av frysing, er gulvarealet delt inn i 4 soner. Bredden på de tre første er 2 meter, og resten refereres til den fjerde.
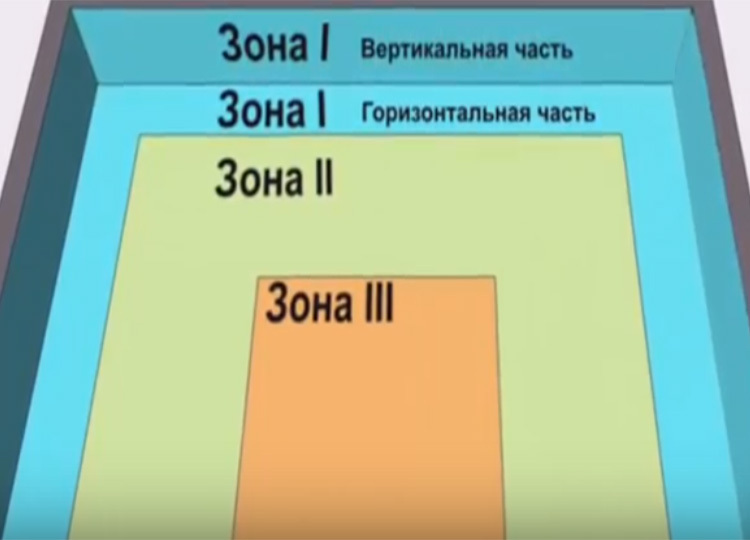
Varmetapssonene i gulvet og kjellergulvet gjentar formen på fundamentets omkrets. De viktigste varmetapene vil gå gjennom sone nr. 1
For hver sone bestemmes motstandskoeffisienten mot varmeoverføring, som tilsettes av jorden:
- sone 1: R1 = 2.1;
- sone 2: R2 = 4.3;
- sone 3: R3 = 8.6;
- sone 4: R4 = 14.2.
Hvis gulvene er isolerte, for deretter å bestemme den totale termiske motstandskoeffisienten, legg sammen indikatorene for isolasjon og jord.
Eksempel. La et hus med yttermål på 10 × 8 m og en veggtykkelse på 0,3 meter ha en kjeller, 2,7 meter dyp. Taket er på bakkenivå. Det er nødvendig å beregne varmetapet til jorda ved den indre lufttemperaturen "+25 ° С", og den eksterne - "–15 ° С".
La veggene være laget av FBS -blokker, 40 cm tykke (λf = 1.69). Fra innsiden er de kledd med et brett, 4 cm tykt (λd = 0.18). Kjellergulvet er fylt med ekspandert leirebetong, 12 cm tykt (λTil = 0.70). Da er termisk motstandskoeffisient for kjellerveggene: Rmed = 0,4 / 1,69 + 0,04 / 0,18 = 0,46, og kjønn RNS = 0.12 / 0.70 = 0.17.
Husets innvendige dimensjoner vil være 9,4 × 7,4 meter.

Ordningen med å dele kjelleren i soner for problemet som skal løses. Å beregne områder med en så enkel geometri kommer til å bestemme sidene av rektangler og multiplisere dem
La oss beregne arealene og varmeoverføringsmotstandskoeffisientene etter soner:
- Sone 1 går bare langs veggen. Den har en omkrets på 33,6 m og en høyde på 2 m. Derfor S1 = 33.6 × 2 = 67.2. Rh1 = Rmed + R1 = 0.46 + 2.1 = 2.56.
- Sone 2 på veggen. Den har en omkrets på 33,6 m og en høyde på 0,7 m. Derfor S2c = 33.6 × 0.7 = 23.52. Rs2s = Rmed + R2 = 0.46 + 4.3 = 4.76.
- Sone 2 etter etasje. S2p = 9.4 × 7.4 – 6.8 × 4.8 = 36.92. Rz2p = RNS + R2 = 0.17 + 4.3 = 4.47.
- Sone 3 går bare langs gulvet. S3 = 6.8 × 4.8 – 2.8 × 0.8 = 30.4. Rh3 = RNS + R3 = 0.17 + 8.6 = 8.77.
- Sone 4 går bare langs gulvet. S4 = 2.8 × 0.8 = 2.24. Rh4 = RNS + R4 = 0.17 + 14.2 = 14.37.
Varmetap i kjellergulvet Q = (S1 / Rh1 + S2c / Rs2s + S2p / Rz2p + S3 / Rh3 + S4 / Rh4) × dT = (26,25 + 4,94 + 8,26 + 3,47 + 0,16) × 40 = 1723 W.
Regnskap for uoppvarmede lokaler
Ofte, når man beregner varmetap, oppstår det en situasjon når det er et uoppvarmet, men isolert rom i huset. I dette tilfellet skjer energioverføring i to trinn. Vurder denne situasjonen ved å bruke eksemplet på et loft.
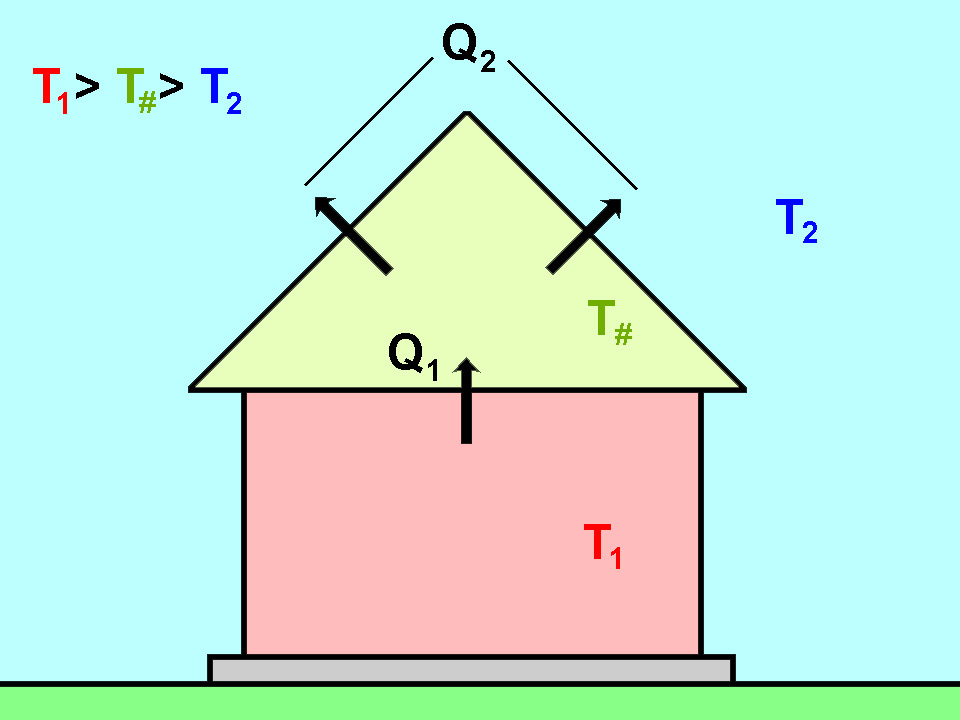
I et isolert, men ikke oppvarmet loftsrom, i den kalde perioden, er temperaturen satt høyere enn utenfor. Dette skyldes overføring av varme gjennom gulvet.
Hovedproblemet er at gulvarealet mellom loftet og overetasjen er forskjellig fra taket og gavlene. I dette tilfellet er det nødvendig å bruke varmeoverføringsbalansen Sp1 = Sp2.
Det kan også skrives på følgende måte:
K1 × (T1 - T#) = K2 × (T# - T2),
hvor:
- K1 = S1 / R1 + … + Sn / Rn å overlappe mellom den varme delen av huset og kjølerommet;
- K2 = S1 / R1 + … + Sn / Rn for overlapping mellom et kjølerom og gaten.
Fra likheten mellom varmeoverføring finner vi temperaturen som vil bli etablert i et kjølerom ved kjente verdier i huset og på gaten. T# = (K1 × T1 + K2 × T2) / (K1 + K2). Etter det erstatter vi verdien i formelen og finner varmetapet.
Eksempel. La husets indre størrelse være 8 x 10 meter. Takvinkelen er 30 °. Lufttemperaturen i lokalene er "+25 ° С", og utenfor - "–15 ° С".
Takets termiske motstandskoeffisient beregnes som i eksemplet gitt i avsnittet for beregning av varmetap gjennom innelukkende strukturer: RNS = 3.65. Overlappingsområdet er 80 m2, derfor K1 = 80 / 3.65 = 21.92.
Takområde S1 = (10 × 8) / cos(30) = 92.38. Vi beregner koeffisienten for termisk motstand, med tanke på tykkelsen på treverket (lathing og etterbehandling - 50 mm) og mineralull (10 cm): R1 = 2.98.
Vindusområde for gavl S2 = 1,5. For vanlige doble vinduer, termisk motstand R2 = 0,4. Pedimentets område beregnes med formelen: S3 = 82 × tg(30) / 4 – S2 = 7.74. Motstandskoeffisienten mot varmeoverføring er den samme som taket: R3 = 2.98.
Varmeavledning gjennom vinduer utgjør en betydelig del av alle energitap. Derfor, i regioner med kalde vintre, bør du velge "varme" doble vinduer
La oss beregne koeffisienten for taket (ikke glem at antallet gavler er to):
K2 = S1 / R1 + 2 × (S2 / R2 + S3 / R3) = 92.38 / 2.98 + 2 × (1.5 / 0.4 + 7.74 / 2.98) = 43.69.
La oss beregne lufttemperaturen på loftet:
T# = (21,92 × 25 + 43,69 × (–15)) / (21,92 + 43,69) = –1,64 ° С.
Erstatt den resulterende verdien i en av formlene for beregning av varmetap (forutsatt at de er like i balanse), og vi får ønsket resultat:
Sp1 = K1 × (T1 – T#) = 21,92 × (25 - (–1,64)) = 584 W.
Kjøling gjennom ventilasjon
Ventilasjonssystemet er installert for å opprettholde et normalt mikroklima i huset. Dette fører til tilsig av kald luft til rommet, som også må tas i betraktning ved beregning av varmetap.
Krav til ventilasjonsvolum er beskrevet i flere forskriftsdokumenter. Når du designer et hussystem for hytter, må du først og fremst ta hensyn til kravene i §7 SNiP 41-01-2003 og §4 SanPiN 2.1.2.2645-10.
Siden den allment aksepterte enheten for måling av varmetap er watt, varmekapasiteten til luft c (kJ / kg × ° С) må reduseres til dimensjonen “W × h / kg × ° С”. For luft på havnivå kan du ta verdien c = 0,28 W × t / kg × ° С.
Siden ventilasjonsvolumet måles i kubikkmeter i timen, er det også nødvendig å kjenne lufttettheten q (kg / m3). Ved normalt atmosfæretrykk og gjennomsnittlig luftfuktighet kan denne verdien tas q = 1,30 kg / m3.

Husholdningsventilasjon med recuperator. Det deklarerte volumet, som det passerer, er gitt med en liten feilmargin. Derfor gir det ingen mening å nøyaktig beregne tettheten og varmekapasiteten til luft på bakken til hundredeler.
Energiforbruket for kompensasjon for varmetap som følge av ventilasjon kan beregnes ved hjelp av følgende formel:
Q = L × q × c × dT = 0,364 × L × dT,
hvor:
- L - luftforbruk (m3 / h);
- dT - temperaturforskjell mellom rom og innkommende luft (° С).
Hvis kald luft kommer inn i huset direkte, så:
dT = T1 - T2,
hvor:
- T1 - innetemperatur;
- T2 - temperaturen ute.
Men for store gjenstander er ventilasjonssystemet vanligvis integrere recuperatoren (varmeveksler). Det lar deg spare energiressurser betydelig, siden delvis oppvarming av innkommende luft skjer på grunn av temperaturen i den utgående strømmen.
Effektiviteten til slike enheter måles i effektiviteten k (%). I dette tilfellet vil den forrige formelen ha formen:
dT = (T1 - T2) × (1 - k / 100).
Beregning av gassforbruk
Å vite totalt varmetap, kan du ganske enkelt beregne det nødvendige forbruket av naturlig eller flytende gass for oppvarming av et hus med et areal på 200 m2.
Mengden energi som frigjøres, i tillegg til drivstoffvolumet, påvirkes av forbrenningsvarmen. For gass er denne indikatoren avhengig av fuktighetsinnholdet og den kjemiske sammensetningen av den medfølgende blandingen. Skill mellom de høyeste (Hh) og lavere (Hl) brennverdi.
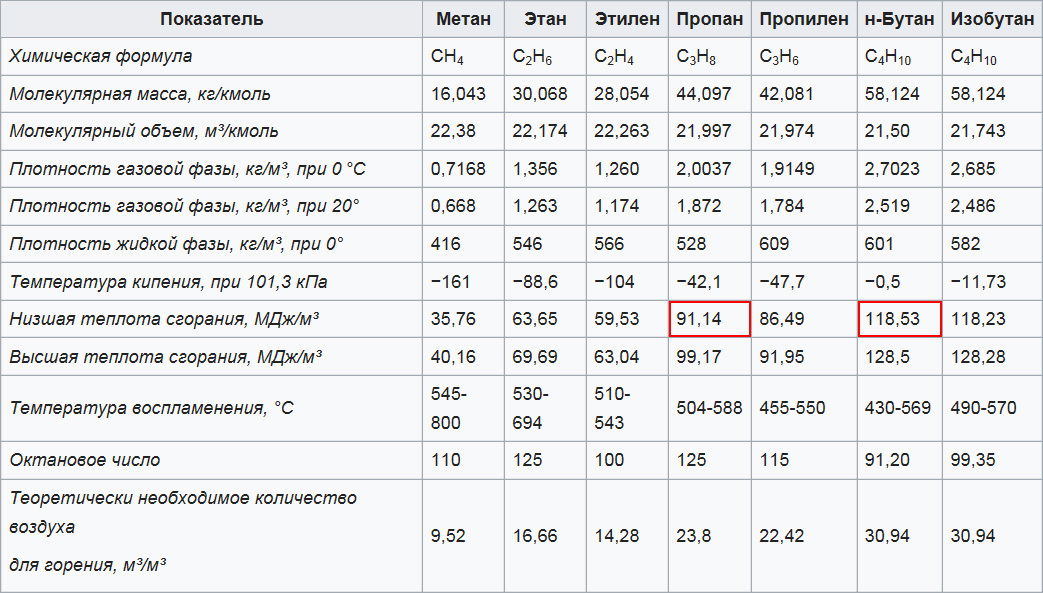
Den lavere brennverdi av propan er mindre enn butan. Derfor, for å nøyaktig bestemme brennverdi av flytende gass, må du vite prosentandelen av disse komponentene i blandingen som leveres til kjelen.
For å beregne mengden drivstoff som garantert vil være nok til oppvarming, erstattes verdien av netto brennverdi i formelen, som kan fås fra gassleverandøren. Standardenheten for brennverdi er "mJ / m3”Eller“ mJ / kg ”. Men siden måleenhetene for både kraften til kjeler og varmetap opererer med watt, og ikke joule, er det nødvendig å utføre en konvertering, med tanke på at 1 mJ = 278 W × h.
Hvis verdien av blandingens netto brennverdi er ukjent, er det tillatt å ta følgende gjennomsnittstall:
- for naturgass Hl = 9,3 kW × t / m3;
- for flytende gass Hl = 12,6 kW × t / kg.
En annen indikator som kreves for beregninger er kjeleeffektiviteten. K. Det måles vanligvis som en prosentandel. Den endelige formelen for gassforbruk over en periode E h) har følgende skjema:
V = Q × E / (Hl × K / 100).
Perioden da sentralisert oppvarming i hus slås på, bestemmes av gjennomsnittlig daglig lufttemperatur.
Hvis den i løpet av de siste fem dagene ikke overstiger "+ 8 ° C", må dekningen av varme til huset sikres i henhold til dekretet fra regjeringen i Den russiske føderasjon nr. 307 av 13.05.2006. For private hus med autonom oppvarming brukes disse tallene også ved beregning av drivstofforbruk.
De nøyaktige dataene om antall dager med en temperatur som ikke er høyere enn “+ 8 ° C” for området der hytta er bygd, kan fås fra den lokale avdelingen i Hydrometeorological Center.
Hvis huset ligger i nærheten av en stor bebyggelse, er det lettere å bruke bordet. 1. SNiP 23-01-99 (kolonne nummer 11). Multiplisere denne verdien med 24 (timer i døgnet) får vi parameteren E fra ligningen for beregning av gassstrømningshastigheten.
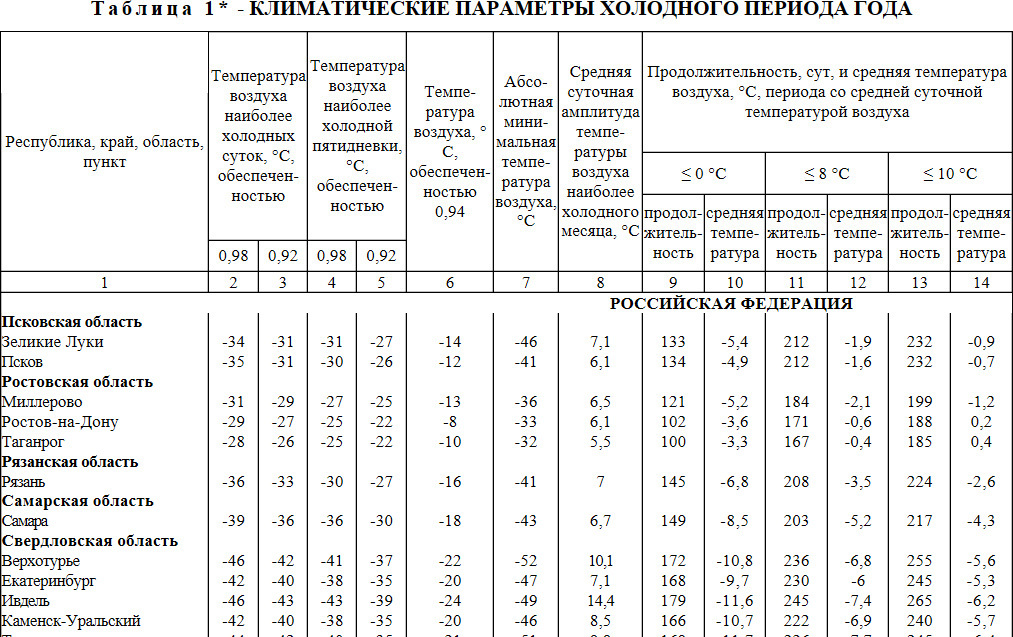
Ifølge klimatiske data fra tabellen. 1 SNiP 23-01-99 konstruksjonsorganisasjoner utfører beregninger for å bestemme varmetapet i bygninger
Hvis luftmengden og temperaturen inne i lokalene er konstant (eller med små svingninger), så varmetap både gjennom de omsluttende konstruksjonene og på grunn av ventilasjon av lokalene vil være direkte proporsjonal med temperaturen uteluft.
Derfor, for parameteren T2 i ligningene for beregning av varmetap, kan du ta verdien fra kolonne nr. 12 i tabellen. 1. SNiP 23-01-99.
Eksempel på en 200 m hytte2
La oss beregne gassforbruket for en hytte nær byen. Rostov ved Don. Oppvarmingstid: E = 171 × 24 = 4104 t. Gjennomsnittlig utetemperatur T2 = - 0,6 ° C. Ønsket temperatur i huset: T1 = 24 ° C.
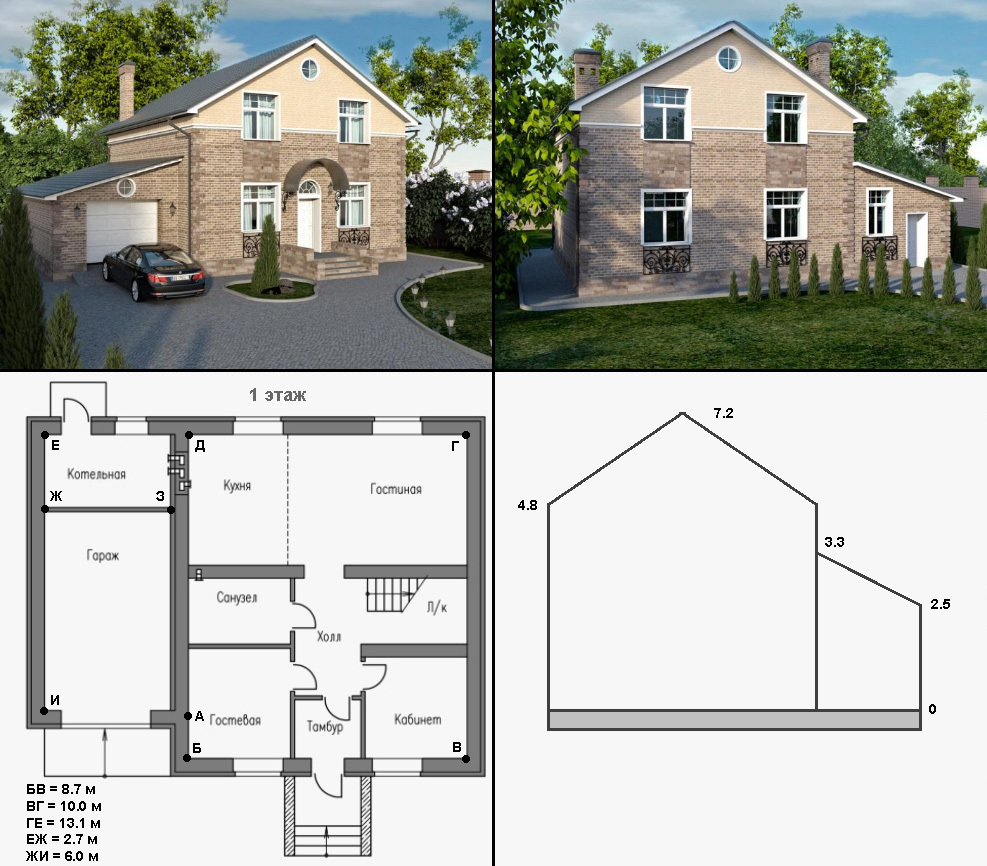
Hytte i to etasjer med uoppvarmet garasje. Det totale arealet er ca 200 m2. Veggene er ikke i tillegg isolerte, noe som er tillatt for klimaet i Rostov -regionen
Trinn 1. La oss beregne varmetapet gjennom omkretsen uten å ta hensyn til garasjen.
For å gjøre dette, velg homogene områder:
- Vindu. Det er totalt 9 vinduer med en størrelse på 1,6 × 1,8 m, et vindu med en størrelse på 1,0 × 1,8 m og 2,5 runde vinduer med et areal på 0,38 m2 hver og en. Totalt vindusareal: Svindu = 28,60 m2. I henhold til produktpasset Rvindu = 0.55. Deretter Spvindu = 1279 W.
- Dører. Det er 2 isolerte dører 0,9 x 2,0 m i størrelse. Området deres: Sdører = 3,6 m2. I henhold til produktpasset Rdører = 1.45. Deretter Spdører = 61 W.
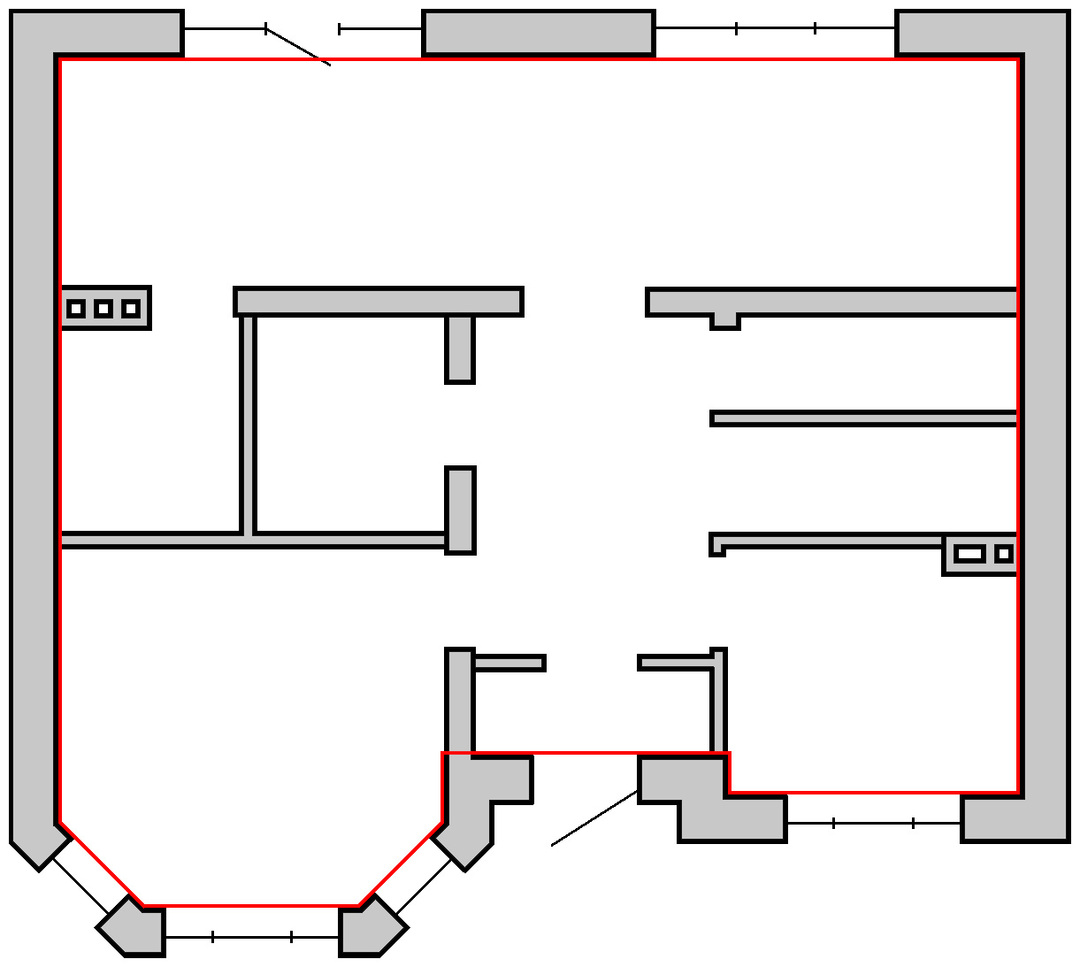
- Tom vegg. Seksjon "ABVGD": 36,1 × 4,8 = 173,28 m2. Plott “JA”: 8,7 × 1,5 = 13,05 m2. Tomt "DEJ": 18,06 moh2. Tak gavlområde: 8,7 × 5,4 / 2 = 23,49. Totalt, tomt veggområde: Svegg = 251.37 – Svindu – Sdører = 219,17 m2. Veggene er laget av 40 cm tykk luftbetong og hule teglstein. Rvegger = 2.50 + 0.63 = 3.13. Deretter Spvegger = 1723 W.
Totalt varmetap gjennom omkretsen:
Spperim = Spvindu + Spdører + Spvegger = 3063 W.
Steg 2. La oss beregne varmetapet gjennom taket.
Isolasjonen er en solid dreiebenk (35 mm), mineralull (10 cm) og fôr (15 mm). Rtak = 2.98. Takflate over hovedbygningen: 2 × 10 × 5,55 = 111 m2, og over fyrrommet: 2,7 × 4,47 = 12,07 m2. Total Stak = 123,07 m2. Deretter Sptak = 1016 W.
Trinn 3. La oss beregne varmetapet gjennom gulvet.
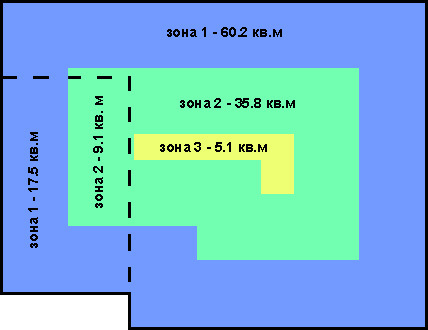
Sonene for det oppvarmede rommet og garasjen må beregnes separat. Området kan bestemmes nøyaktig med matematiske formler, eller du kan bruke vektorredaktører som Corel Draw
Motstand mot varmeoverføring tilbys av grove gulvplater og kryssfiner under laminatet (totalt 5 cm), samt basaltisolasjon (5 cm). Rkjønn = 1.72. Da vil varmetapet gjennom gulvet være likt:
Spgulv = (S1 / (Rgulv + 2.1) + S2 / (Rgulv + 4.3) + S3 / (Rgulv + 2.1)) × dT = 546 W.
Trinn 4. La oss beregne varmetapet gjennom en kald garasje. Gulvet er ikke isolert.
Varme trenger inn fra et oppvarmet hus på to måter:
- Gjennom den bærende veggen. S1 = 28.71, R1 = 3.13.
- Gjennom en murveggskille fra fyrrommet. S2 = 11.31, R2 = 0.89.
Vi får K1 = S1 / R1 + S2 / R2 = 21.88.
Varme kommer ut av garasjen som følger:
- Gjennom vinduet. S1 = 0.38, R1 = 0.55.
- Gjennom porten. S2 = 6.25, R2 = 1.05.
- Gjennom veggen. S3 = 19.68, R3 = 3.13.
- Gjennom taket. S4 = 23.89, R4 = 2.98.
- Gjennom gulvet. Sone 1. S5 = 17.50, R5 = 2.1.
- Gjennom gulvet. Sone 2. S6 = 9.10, R6 = 4.3.
Vi får K2 = S1 / R1 + … + S6 / R6 = 31.40
La oss beregne temperaturen i garasjen, med forbehold om varmeoverføringsbalansen: T# = 9,2 ° C. Da vil varmetapet være likt: Spgarasje = 324 W.
Trinn 5. La oss beregne varmetapet på grunn av ventilasjon.
La det beregnede ventilasjonsvolumet for en slik hytte med 6 personer som bor i det være 440 m3/час. Systemet har en recuperator med en effektivitet på 50%. Under disse forholdene, varmetap: Splufte = 1970 W.
Steg. 6. La oss bestemme det totale varmetapet ved å legge til alle lokale verdier: Sp = 6919 W.
Trinn 7. La oss beregne volumet av gass som kreves for å varme et modellhus om vinteren med en kjeleeffektivitet på 92%:
- Naturgass. V = 3319 moh3.
- Flytende gass. V = 2450 kg.
Etter beregninger kan du analysere de økonomiske kostnadene ved oppvarming og gjennomførbarheten av investeringer for å redusere varmetap.
Konklusjoner og nyttig video om temaet
Varmeledningsevne og motstand mot varmeoverføring av materialer. Beregningsregler for vegger, tak og gulv:
Den vanskeligste delen av beregningene for å bestemme volumet av gass som kreves for oppvarming, er å finne varmetapet til det oppvarmede objektet. Først og fremst må du nøye vurdere geometriske beregninger.
Hvis de økonomiske kostnadene for oppvarming virker overdrevne, bør du tenke på ytterligere isolasjon av huset. Videre viser beregningene av varmetap strukturen til å fryse godt.
Legg igjen kommentarer i blokken nedenfor, still spørsmål om uklare og interessante punkter, legg ut bilder om emnet i artikkelen. Del din egen erfaring med å utføre beregninger for å finne ut kostnadene ved oppvarming. Det er mulig at dine råd i stor grad vil hjelpe besøkende på nettstedet.